統計検定2級の勉強をする話⑧

前回↓
今回は2変数の確率分布、標本分布、中心極限定理について
2変数の確率分布
同時確率分布
2つの確率変数X、Yの取りうる値と確率の対応関係を同時確率分布といい、定義される関数を同時確率関数という。
\[ P(X = x_i, Y = y_j) = p(x_i, y_j) \]
その中で片方の確率分布を示したものを周辺分布といい、その関数を周辺確率関数という。
\[ P(X = x_i) = \sum_j p(x_i, y_j) \]
2つの確率変数の共分散、相関係数
同時確率分布の期待値はそれぞれの確率変数の期待値の和に等しい。
\[ E[X + Y] = E[X] + E[Y] \]
なので分散は
\[ \text{Var}(X + Y) = \text{Var}(X) + \text{Var}(Y) + 2(E[XY] - E[X]E[Y]) \]
となる。ここで第3項が共分散
\[ \text{Covariance} =2(E[XY] - E[X]E[Y]) \]
であり、共分散とそれぞれの分散から相関係数が導ける。
\[ \rho(X, Y) = \frac{\text{Covariance}(X, Y)}{\sqrt{\text{Var}(X) \cdot \text{Var}(Y)}} \]
2変量正規分布
2つの連続型確率関数が正規分布に従うとき、その同時確率密度関数は
\[ f(x, y) = \frac{1}{2\piσ_Xσ_Y\sqrt{1-\rho^2}} \exp\left(-\frac{1}{2(1-\rho^2)}\left[\frac{(x-\mu_X)^2}{σ_X^2} + \frac{(y-\mu_Y)^2}{σ+_Y^2} - \frac{2\rho(x-\mu_X)(y-\mu_Y)}{σ_Xσ_Y}\right]\right) \]
で表される
これを3次元上で示すと、あらゆるx、yの条件付き分布が正規分布に従うことがわかる。
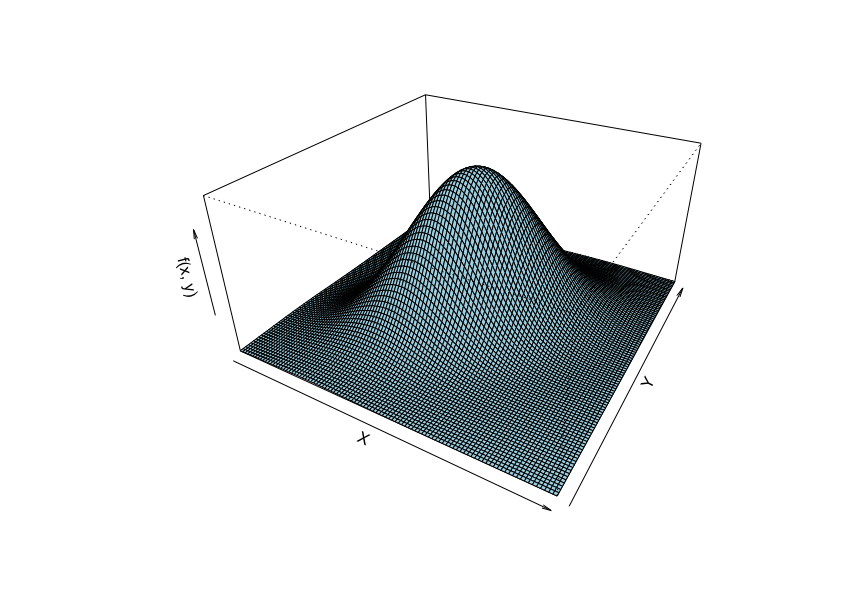
その正規分布の期待値と分散は
\[ E[Y | X = x] = \mu_Y + \rho \frac{σ_Y}{σ_X} (x - \mu_X) \]
\[ \text{Var}(Y | X = x) = σ_Y^2 (1 - \rho^2) \]
標本分布
母集団から無作為標本を抽出したときの統計量の確率分布を標本分布という。
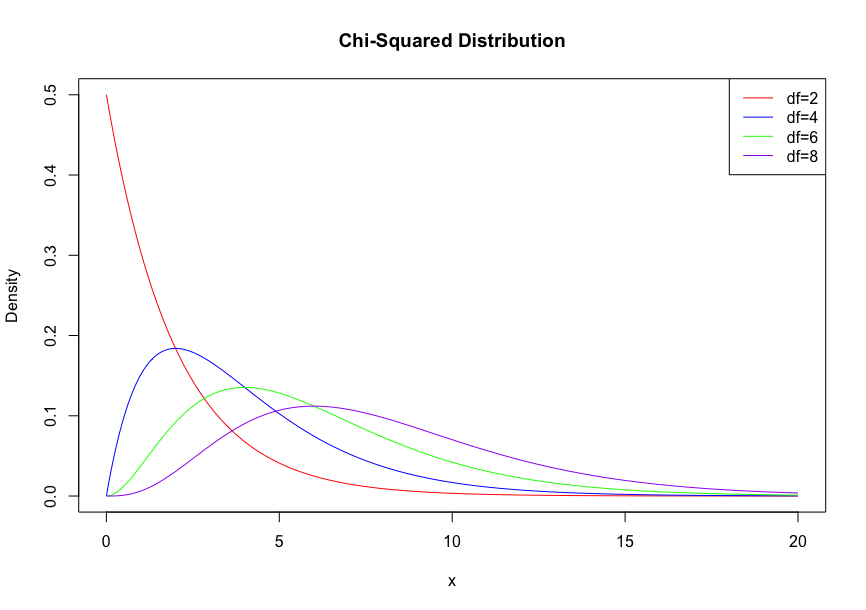
\( χ^2\)分布
複数の確率変数が互いに独立で、標準正規分布に従うときのそれぞれの確率変数の2乗の和の分布。
確率変数の数nを自由度という。
その期待値と分散は
\[ E[X] = n \]
\[ \text{Var}(X) = 2n \]
となる
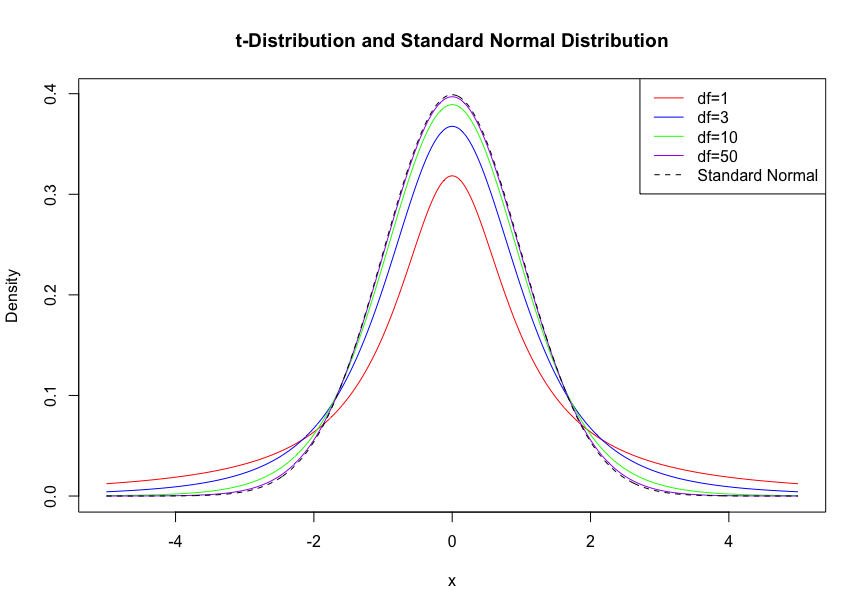
t分布
独立な2つの確率変数において、片方が標準正規分布、もう片方が自由度nの\( χ^2\)分布に従う時、
\[ t = \frac{Z}{\sqrt{W/n}} \]
の分布をt分布という。
その期待値、分散は
\[ E[T] = \begin{cases} 0 & \text{if } n > 1 \\ \text{undefined} & \text{if } n \leq 1 \end{cases} \]
\[ \text{Var}(T) = \begin{cases} \frac{n}{n - 2} & \text{if } n > 2 \\ \infty & \text{if } 1 < n \leq 2 \\ \text{undefined} & \text{if } n \leq 1 \end{cases} \]
自由度を大きくすると標準正規分布に近づく
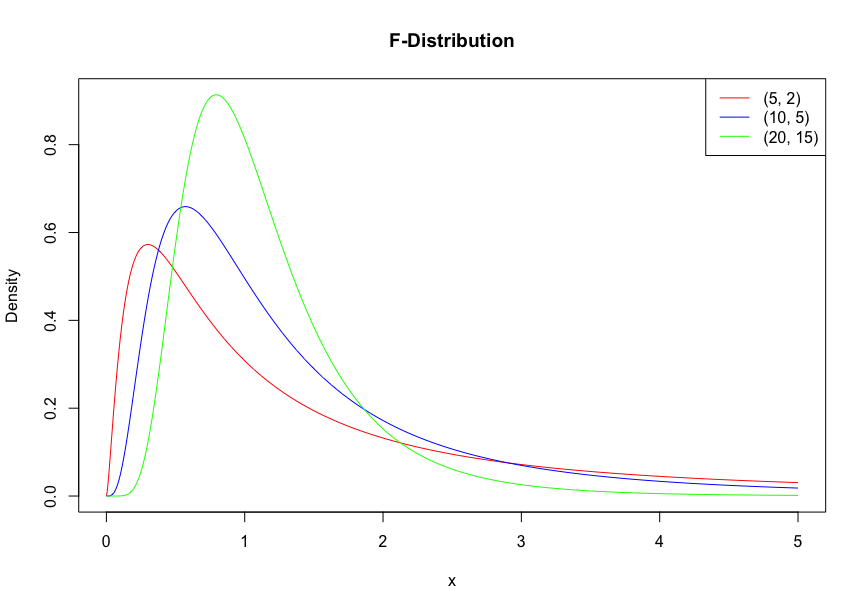
F分布
独立に自由度N1、N2の\( χ^2\)分布に従う確率変数W1、W2がある時、
\[ F = \frac{W_1/N_1}{{W_2/N_2}} \]
の従う分布をF分布という。
大数の法則と中心極限定理
なんか結構前に一回勉強した気がするからざっくり。
大数の法則(弱法則)
以下に示すチェビシェフの不等式は任意の確率変数に対して、上限と下限を設けることができる。
\[ P(|X - \mu| \geq kσ) \leq \frac{1}{k^2} \]
これを標本平均に対して考え、nを無限に大きくすると、
\[ \forall \epsilon > 0, \lim_{{n \to \infty}} P\left(|\bar{X}_n - \mu| \geq \epsilon\right) = 0 \]
となり、標本平均は母平均に収束する。
中心極限定理
nが大きい場合、元の分布が正規分布に従わない場合でもその平均は正規分布に近づく。
そして母集団の平均がμ、標準偏差がσ、標本サイズがnの時標本集団の平均はμ、標準偏差σ/√nに従う。
今日はここまで。
標本分布に関してはイマイチどう実用できるのかわからん。