機械学習の評価指標を学ぶ

統計検定も落ち着いたので、ぼちぼち機械学習の勉強も再開したい。

回帰問題の評価指標
二値分類の評価指標(正例である確率が予測値の場合)
- logloss(cross entropy)
- AUC(Area Under the ROC curve)
マルチクラス分類の評価指標
- quadratic weighted kappa
レコメンデーションの評価指標
- MAP@K

こちら過去五年のKaggleコンペの主要指標

LogLoss
AUC
WeightedMeanColumnwiseLogLoss
QuadraticWeightedKappa
OpenImagesObjectDetectionAP
MWCRMSE
MCAUC
MAP@K
Jaccard

回帰問題の評価指標

RMSE:Root Mean Squared Error

$$ \text{RMSE} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2} $$

平均二乗誤差の平方根。

def rmse_sklearn(predictions, targets):
    mse = mean_squared_error(targets, predictions)
    return np.sqrt(mse)

＊外れ値の影響を受けやすい

＊目的変数の平方根をとってMSEを目的関数として学習して適合できる

RMSLE:Root Mean Squared Logarithmic Error

$$ \text{RMSLE} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (\log(1 + y_i) - \log(1 + \hat{y}_i))^2} $$

予測値と実測値の対数の差の二乗の平均の平方値

def rmsle(y_true, y_pred):
    return np.sqrt(mean_squared_log_error(y_true, y_pred))

＊目的変数の対数を新たな目的変数としてRMSEを実施しているのと同じ。

＊目的変数が裾の重い分布を撮る時に有用

＊予測値の差は重要ではなく、尺度が実測値と同じかどうかが重要

MAE:Mean Absolute Error

$$ \text{MAE} = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i| $$

実測値と予測値の差の絶対値の平均

def mae(actual, predicted):
    return np.mean(np.abs(actual - predicted))

＊外れ値の影響を受けにくい

＊計算時間長くなりがち

＊予測値＝実測値で微分不可能なので勾配ブースティングなどが使用できない。

そのため損失関数には近似関数としてfair関数やPseudo-Huber関数を用いる必要がある。

<fair関数>

def fair_function(x, c=1.0):
    return c**2 * (np.abs(x)/c - np.log(1 + np.abs(x)/c))

<Pseudo-Huber関数>

def pseudo_huber_function(x, delta=1.0):
    return delta**2 * (np.sqrt(1 + (x/delta)**2) - 1)

二値分類の評価指標(正例である確率が予測値の場合)

logloss(cross entropy)

\[logloss = -\frac{1}{N} \sum_{i=1}^{N} [y_i \log(p_i) + (1 - y_i) \log(1 - p_i)]\]

正負の予測の確率をより大きく外すと損失が大きくなるようになっている

from sklearn.metrics import log_loss
loss = log_loss(y_true, y_pred)

AUC(Area Under the ROC curve)

ROC曲線の面積

予測値を正例とする閾値を１から０にしたときの偽陽性率と真陽性率をプロットしたグラフ

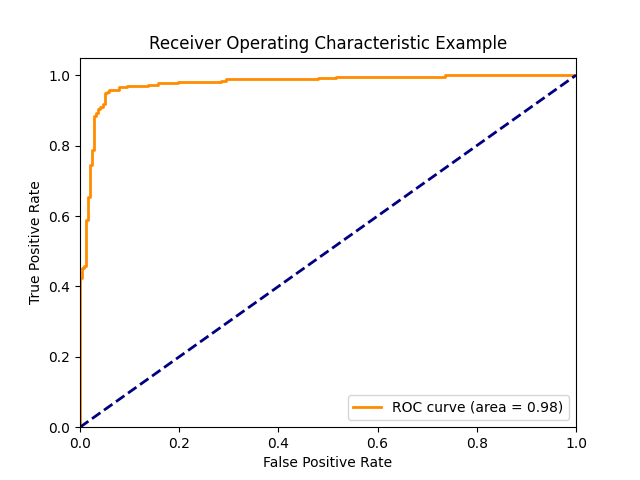
from sklearn.metrics import roc_auc_score
auc = roc_auc_score(y_true, y_pred)

＊青点線は完全ランダムの場合で、AUCは0.5になる

＊予測値の大小関係のみが影響するため、必ずしも確率である必要はなく、別の指標を用いても良い。

＊負例の予測より正例の予測の誤差の方が影響を受けやすい。

＊Gini係数とは線形関係

マルチクラス分類の評価指標

quadratic weighted kappa

クラス間に順序関係がある場合に用いる

$$ \kappa = 1 - \frac{\sum_{i,j}w_{ij}o_{ij}}{\sum_{i,j}w_{ij}e_{ij}} $$

from sklearn.metrics import cohen_kappa_score
kappa = cohen_kappa_score(rater1, rater2, weights='quadratic')

完全に予測すると1、ランダムだと0、それ以下だと負の値を取る。

レコメンデーションの評価指標

MAP@K

$$ MAP@K = \frac{1}{Q} \sum_{q=1}^{Q} \left( \frac{1}{\min(m_q, K)} \sum_{k=1}^{K} \text{Precision}(k) \times \text{rel}_q(k) \right) $$

def average_precision_at_k(actual, predicted, k):
    if not actual:
        return 0.0

    score = 0.0
    num_hits = 0.0

    for i, p in enumerate(predicted[:k]):
        if p in actual and p not in predicted[:i]:
            num_hits += 1.0
            score += num_hits / (i + 1.0)

    return score / min(len(actual), k)

def map_at_k(actual, predicted, k):
    return sum(average_precision_at_k(a, p, k) for a, p in zip(actual, predicted)) / len(actual)